

The idea of filtration is a generalization of many types of data that we find in real applications. In particular, we can think about filtrations as:
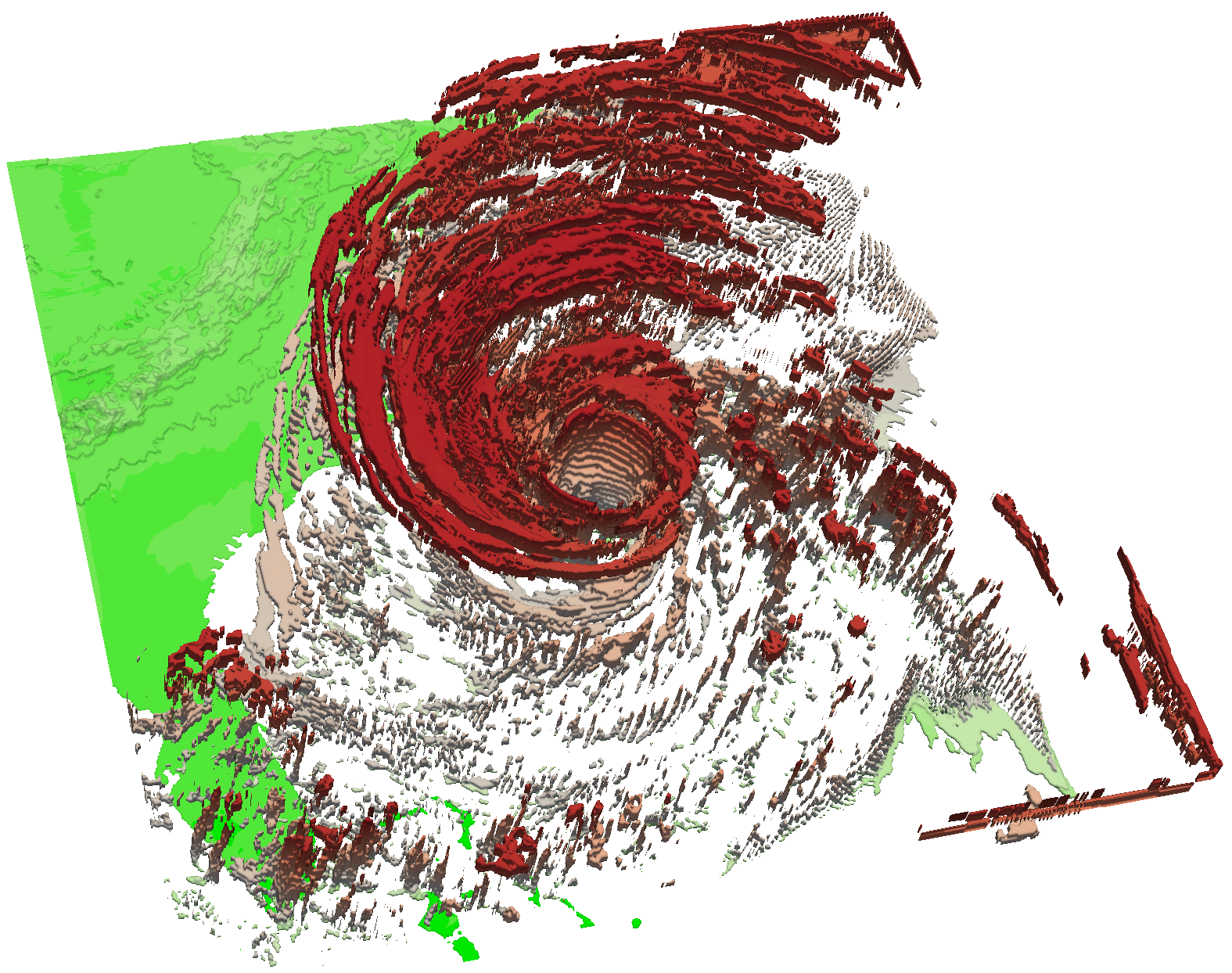 Figure 3 - A simulation of the Hurrican Isable.
Figure 3 - A simulation of the Hurrican Isable.
Scalar fields. When dealing with scalar fields, a function \(f\) is defined on the vertices of an input complex \(\Sigma\). In such cases, the filtering function on \(\Sigma\) is obtained by assigning to each simplex of \(\Sigma\) the maximum among the values of its vertices. Formally, given a simplex \(\sigma\) of \(\Sigma\), the function value \(f(\sigma)\) is usually defined as \(max \{f(v) \,|\, v \text{ is a vertex of } \sigma\}\).
In practical applications, scalar fields are extremely common. The simplest examples of scalar fields are arguably the terrain datasets. A terrain dataset can be considered as a planar triangulation where each point is defined by two coordinates. The scalar function defined for each of theme is also called elevation in this case. Volumetric images are other examples of scalar fields. These types of datasets can be described as point clouds immersed in the 3D space. The regular distribution of the points naturally infers a topology on them. Volumetric images are common in medicine (3D TAC or MRI machines produces this kind of data) or scientific simulations used in engineer or forecast analysis.
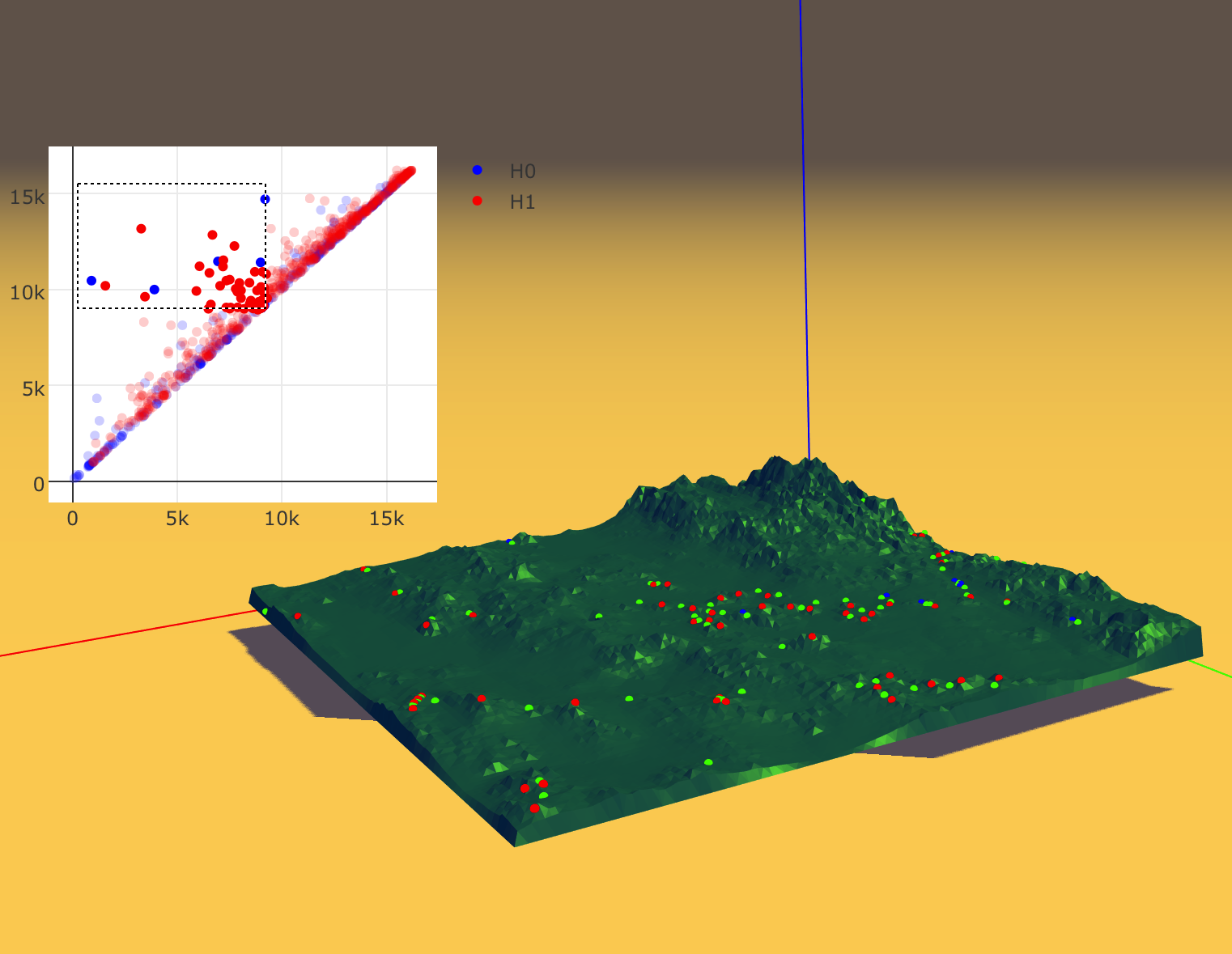 Figure 4 - A terrain dataset analyzing using our visual tool .
Figure 4 - A terrain dataset analyzing using our visual tool .
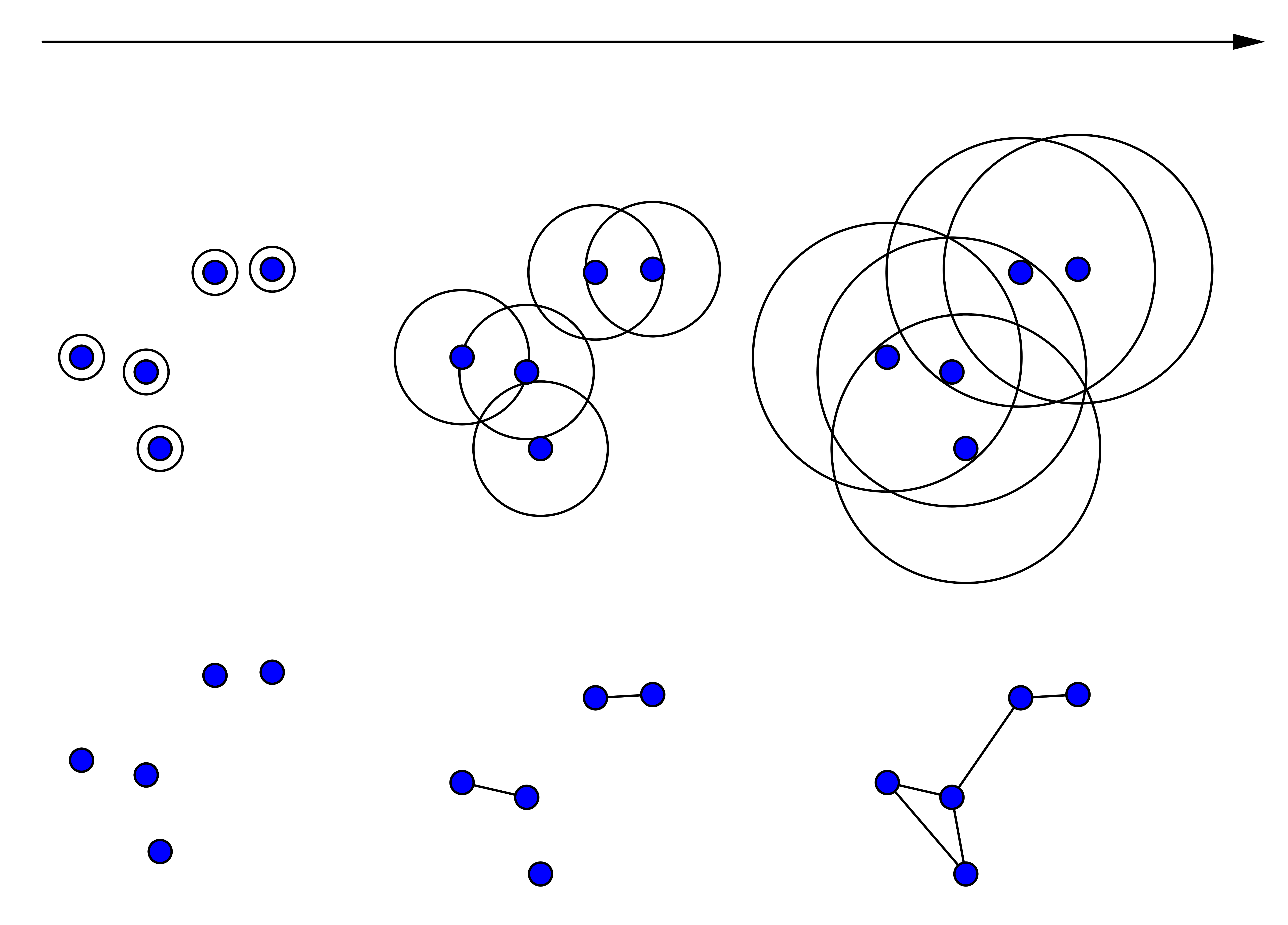 Figure 5 - Filtration based on a distance function computed between pairs of points.
Figure 5 - Filtration based on a distance function computed between pairs of points.
Point clouds. Point cloud data are extremely common in the applications. Defined as set of points embedded in some space (possibly high dimensional), the analysis of point clouds is one of the most classical examples where persistent homology has been applied. When working with point clouds, the simplicial complex is built directly on the input data by defining a "distance" function. One of the most famous approaches for defining such a complex is the Vietoris-Rips. The Vietoris-Rips complex at scale \(\epsilon\) is an abstract simplicial complex \(\Sigma\) obtained defining a distance function \(d(v_1,v_2)\) such that each simplex of \(\Sigma\) has vertices that are pairwise within distance \(d(v_1,v_2) < \epsilon\). In real applications, given the input point cloud, a sequence of growing simplicial complexes is built by incrementing the parameter \(\epsilon\). This creates a filtration which homology changes can be studied using persistent homology. Actually, the techniques used for building such a sequence are quite different, but all of them are based on an increasing distance value \(d\). A connection between two distinct points is established once their distance is less than the threshold value \(d\). Classical constructions that have to be mentioned are:
In our description, we have focused our attention on the first algorithm defined in the literature for computing persistent homology. We have denoted it as the standard algorithm. Its time complexity is potentially super-cubical in the number of the simplices of the simplicial complex \(\Sigma\) but, in practical cases, can be considered linear. Despite this, in the literature several approaches improving the described algorithm have been developed to compute homology and persistent homology. Based on the strategy they adopt, we can subdivide the methods introduced in the literature to retrieve homological information into the following classes:
2. Distributed approaches efficiently retrieve the homological information of a complex through parallel and distributed computations. Some of such approaches are based on a decomposition of the simplicial complex, while others act directly on the boundary matrices. In the literature, several methods have adopted such a distributed strategy: by using spectral sequences, by parallelizing a coreduction-based algorithm, by decomposing the boundary matrix in chunks or by exploiting a distributed memory environment.
3. Recently, a new strategy of computation is revealing very efficient. In this case, persistent homology is efficiently retrieved by the use of annotations which are vectors associated with each simplex of the complex encoding in a compact way the homology class of the simplex itself.
A different and fundamental subfield of methods studied for seeking of efficiency while computing persistent homology are the so-called, coarsening or pruning approaches. These methods reduce the size of the input complex without changing its homological information by applying iterative simplifications, and by computing the persistent homology when no more simplification is possible. Some of these approaches are based on reductions and coreductions, others simplify the simplicial complex via acyclic subspaces or by using edge contractions. Similar approaches are based on the notion of tidy set, a minimal simplicial set obtained trimming and thinning the original simplicial complex, or on the construction of the discrete Morse complex, a compact model homologically-equivalent to the input complex.