

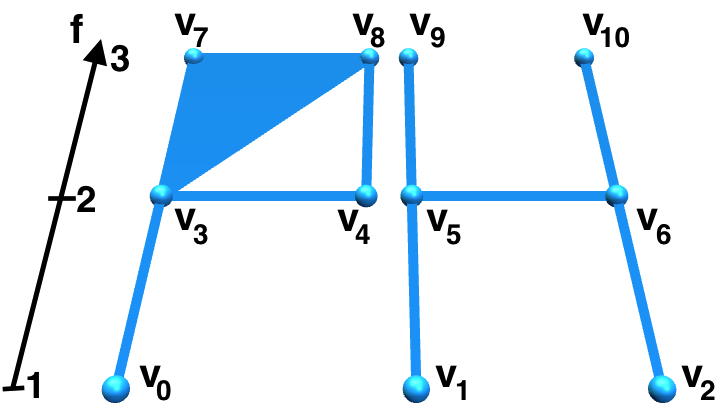
Let \(m\) be a natural number. A filtering function is a function \(f:\Sigma\longrightarrow \{1, \dots, m\}\) such that, for each \(k\)-simplex \(\sigma\) and each \(0\leq i\leq k\), it holds that \(f(\hat{\sigma}_i)\leq f(\sigma)\). The filtering function \(f\) induces a nested sequence of simplicial complexes called filtration and denoted by \(\Sigma^f\) $$ \Sigma^f\quad :\quad \emptyset=:\Sigma^{0}\subseteq\dots\subseteq\Sigma^{m}=\Sigma $$ where, for each \(0\leq p\leq m\), the simplicial subcomplex \(\Sigma^{p}\) is defined by $$ \Sigma^{p}:=\{ \sigma\in\Sigma\ |\ f(\sigma)\leq p \} $$
The main goal of persistent homology consists in studying the filtration and, in particular, tracking the homologies that appear and disapper. Let us choose two parameters \(p\leq q\) of the filtration and a homology degree \(k\). Since the filtration has nested complexes, we will have that $$Z_k(\Sigma^{p})\subseteq Z_k(\Sigma^{q})$$ and $$B_k(\Sigma^{p})\subseteq B_k(\Sigma^{q})$$ Moreover, we get induced a linear map \(i_k^{p,q}:H_k(\Sigma^{p})\longrightarrow H_k(\Sigma^{q})\) between the two different homology spaces.
Given the filtration \(\Sigma^f\), the \((p,q)\)-persistent \(k\)-homology space is defined by $$ H^{p,q}_k(\Sigma^f):=\mbox{Im}(i_k^{p,q}) $$ That is, \(H^{p,q}_k(\Sigma^f)\) is the subspace of \(H_k(\Sigma^{q})\) of the homology classes already born at parameter \(p\) which persist at parameter \(q\).
A persistence class for a filtration \(\Sigma^f\) is a homology class \(h\) belonging to \(H_k(\Sigma^p)\) for at least one parameter \(p\). We associate \(h\) with the smallest parameter \(p_h\) where it exists in the filtration and we say that \(h\) is born at level \(p_h\).
By increasing parameter \(p\), the class \(h\) cannot split into two different classes since the complexes in \(\Sigma^f\) are nested. However, \(h\) can possibly become equivalent to another class \(h'\) at same greater parameter in case some boundary between the two classes enters the filtration.
When \(h\) merges to \(h'\) at parameter \(q\), we say that the homology class dies at level \(q_h\). Generally, we assume that the persistence class dying is the younger one. In case \(p_h=p_{h'}\), both choices are allowed as long as one class dies and the other survives. When a class \(h\) never dies, we assign \(q_h=\infty\).
Persistent homology features are represented by the \(k\)-persistence diagram Dgm\(_k(\Sigma^f)\). The elements in Dgm\(_k(\Sigma^{f})\) are all the persistence pairs \((p_h,q_h)\) in \(\{0, \dots, m\}\times(\{0, \dots, m\}\cup\infty)\) for each persistence class \(h\) of homology degree \(k\) in the filtration \(\Sigma^f\).
Formally speaking, the persistent diagram is not a proper set since each element \((p,q)\) in Dgm\(_k(\Sigma^f)\) can possibly appears many times. The multiplicity of a persistence pair \((p,q)\) is the number of different persistence classes \(h\) such that \((p_h,q_h)=(p,q)\). Hence, the persistence diagram is a multiset.
In case \(q_h=\infty\), the class \(h\) is called essential since, in fact, it is part of the homology of \(\Sigma\). For non-essential classes \(h\), the persistence is its own life duration, that is \(p_h-q_h\). We visualize the persistence of a class in the persistence diagram as the distance of its respective point \((p_h,q_h)\) from the diagonal \(\Delta:=\{ (p,q)\in\{0, \dots, m\}\times\{0, \dots, m\} \ |\ p=q \}\) in the \(\infty\)-norm.
Other tools have been proposed for representing persistent homology.
Barcodes represent a different but equally intuitive way for visualizing peristence pairs. Properly, a barcode is a graphical representation of the persistent homology of a filtered simplicial complex as a collection of horizontal line segments obtained by considering each persistence pair \((p,q)\) as an interval.
Recently, a novel representation for the visualization of persistence pairs, called persistence landscape, has been introduced. A persistence landscape is a representation halfway between the persistence diagram and the barcode. It can be roughly considered as a horizontal version of the persistence diagram and it has been studied for better combining topological data analysis with statistics and machine learning.