Federico Iuricich

Info and News

Email: fiurici@clemson.edu

Address: Clemson University
School of Computing
Visual Computing Division
Mc Adams Hall
Office: 305

Twitter - @IuricichF
GitHub - IuricichF
ResearchGate - Federico Iuricich

CV - (last update 8/20/2018)

Springer book published.

I received my Bachelor and Master degree in Computer Science at the University of Genova, in 2008 and 2010, respectively. I started my PhD in 2011 under the supervision of Professor Leila De FLoriani. During Fall 2012 I've been a visiting PhD student at the University of Maryland collaborating with Kenneth Weiss and, successively, Patricio Simari. In 2014 I got my PhD in Computer Science at the University of Genova defending a thesis on "Multi-resolution shape analysis based on discrete Morse decompositions". From September 2014 to June 2016 I have been a postdoctoral fellow in the Department of Computer Science at the University of Maryland, at College Park. In July 2016 I joined the Geographical Sciences Department as a research fellow working in the Center for Geospatial Information Science focusing in geospatial data analysis and visualization. From January 2018 to July 2018 I have been a visiting researcher at Queens College (City University of New York), working with Dr. Chao Chen at the intersection of machine learning and topological data analysis. Currently I am an assistant professor in the School of Computing at Clemson University.

My research interesets include

• Data visualization:

  scalar field and multivariate data analysis

• Topological Data Analysis:

  discrete Morse theory, persistent homology, multidimensional persistence

• Data structures:

  multiresolution models, simplicial complexes, spatial indexes

I am looking for motivated students to work with. Drop me a line if interested.

Projects

Terrain Modeling

Digital Terrain Models (DTMs) and Digital Surface Models (DSMs), provide a detailed geometric representation of a terrain. Terrain analysis requires extracting succinct descriptors that can capture the broader, higher level structures of the terrain. In my research, I focus on the Forman gradient and discrete Morse complexes as abstract morphological descriptions of a terrain. By using the Forman gradient, we can efficiently compute critical points and integral lines used for creating morphological segmentations. I am particularly interested in developing scalable and efficient methods for triangulations and point data of big size. Current mesh data structures are not feasible for very large data especially if parallelize/distribute the computation is required. In my work, I am using the Morse complexes as an intermediate representation for such purposes.

Highlights

• Computing a Forman gradient requires perturbing the input values so to remove "flat regions" from the input data (areas where vertices have all the same function value). By perturbing we also introduce noise that has to be treated with noise removal techniques. We defined the first method for 2D simplicial complexes (terrain data and 3D triangulated shapes) that does no require data perturbation.
• The Forman gradient can be easily computed in parallel by working in the neighborhood of each vertex of an input dataset. Simplifying the Forman gradient is a much harder task to be performed in parallel. By using the Stellar tree, a spatio-topological data structure developed by my colleague Riccardo Fellegara, we have defined the first efficient method for simplifying a Forman gradient by efficiently subdividing the dataset.

Topology Based Visual analytics

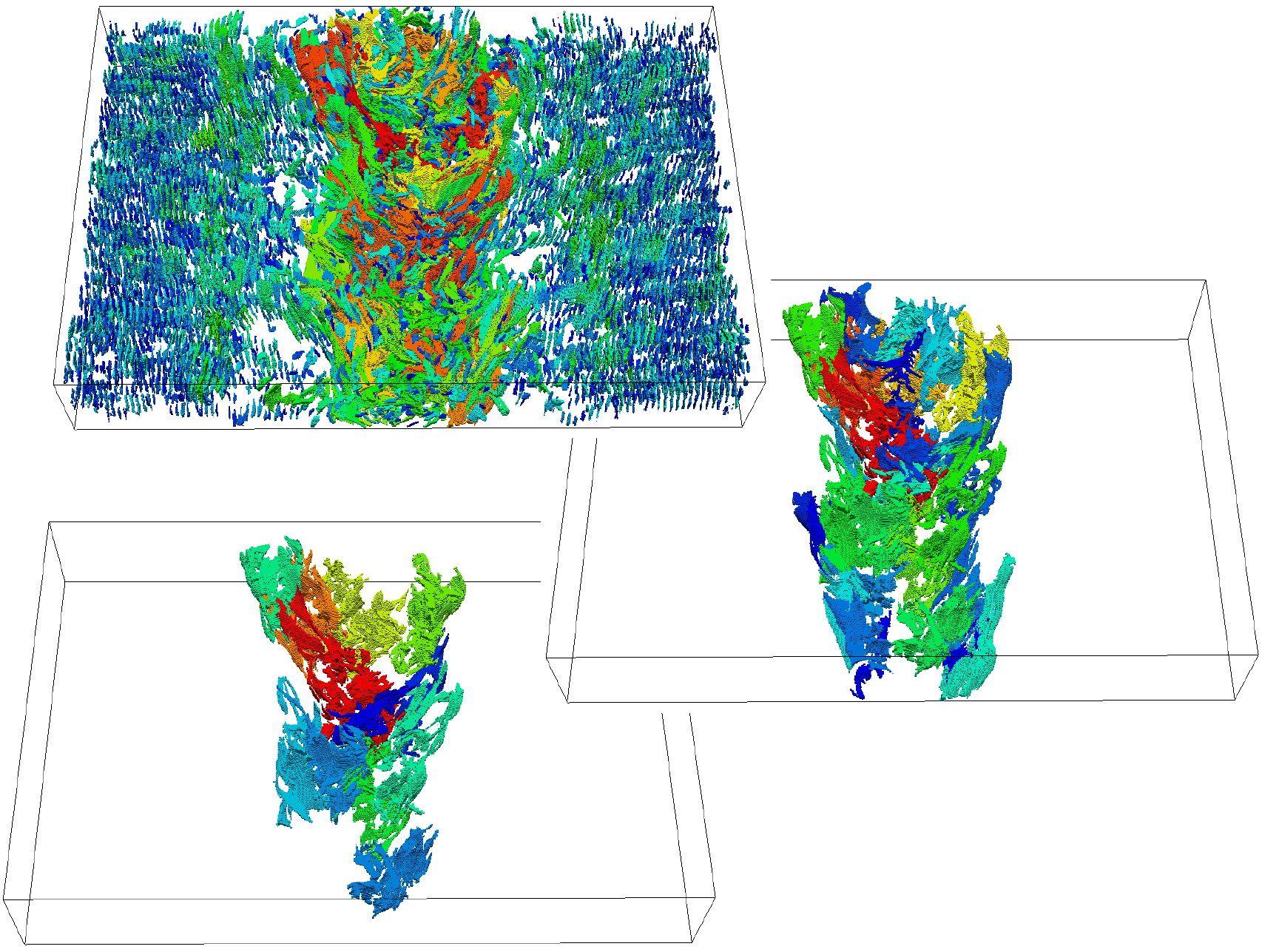Topological Data Analysis relies on tools rooted in computational topology. Based on TDA many visualization tools have been developed for studying the shape of an object or the analyzing the evolution of scalar or vector-valued functions. I am focusing on studying efficient tools for data segmentation, based on persistent homology. The generality of topological tools makes them well suited for any data, either they are scalar fields, point data, multivariate data or vector fields. Recently I have worked on the first algorithm for computing a gradient-based representation on multivariate data. This is the first algorithm capable of extracting a discrete gradient field on real-world data. In my current research, I am studying the relationships between this new gradient based representation and its monodimensional counterpart trying to extend the usefulness of persistent homology to the multidimensional case (i.e., when multiple filtrations are provided).

Highlights

• The use of topological methods in scalar field analysis has been widely explored, but in applications, it is easy to find data described not by a single scalar field, but by multiple scalar fields (also called multivariate data). The use of topology here is at an exploratory stage. In our work, we have defined the first algorithm for computing a discrete vector field on multivariate data. By using the gradient, we can extract visual representations for studying the correlation among the multiple functions.
• Morse-Smale (MS) complexes can be simplified by using an explicit approach, working on the graph representation of the MS complex, or by using an implicit method, which natively works on the Forman gradient. It has been shown that this approach may create topologically-inconsistent representations when operating in three or higher dimensions. We have proposed the first simplification approach that does not present this issue.
• We published two new survey papers, one focusing on topology-based visualization and the other on the use of Morse complexes for shape analysis and visualization.
• While representing Morse complexes on regular data (square and cubical grids) is relatively easy, doing that efficiently on simplicial complexes is a challenging task. We have defined the first compact data structure for representing a Forman gradient on a tetrahedral mesh, effectively. By using a primal/dual argument, we have introduced the first compact representation for a discrete Morse complex defined on a simplicial complex.

High-dimensional data analysis

While several data structures have been proposed in the literature for both cell and simplicial complexes very few of them scale when working in high dimensions. We are working on a new model for encoding a simplicial complex, that we call a Stellar decomposition. The objective is obtaining a compact representation which scales well with both the size and the dimension of the complex. We are developing dedicated versions of the Stellar decomposition to be included in distributed frameworks, such as Hadoop or Apache Spark. I think that being able to represent a simplicial complex efficiently will boost the efficiency in high-dimensional data analysis, which nowadays is mainly limited to the analysis of point clouds or graphs. By developing structures like the Stellar decomposition, my objective is twofold: (i) overcome the current limitations in representing simplicial complexes when working with big data (ii) improving the efficiency of extracting structural information of high-dimensional data

Highlights

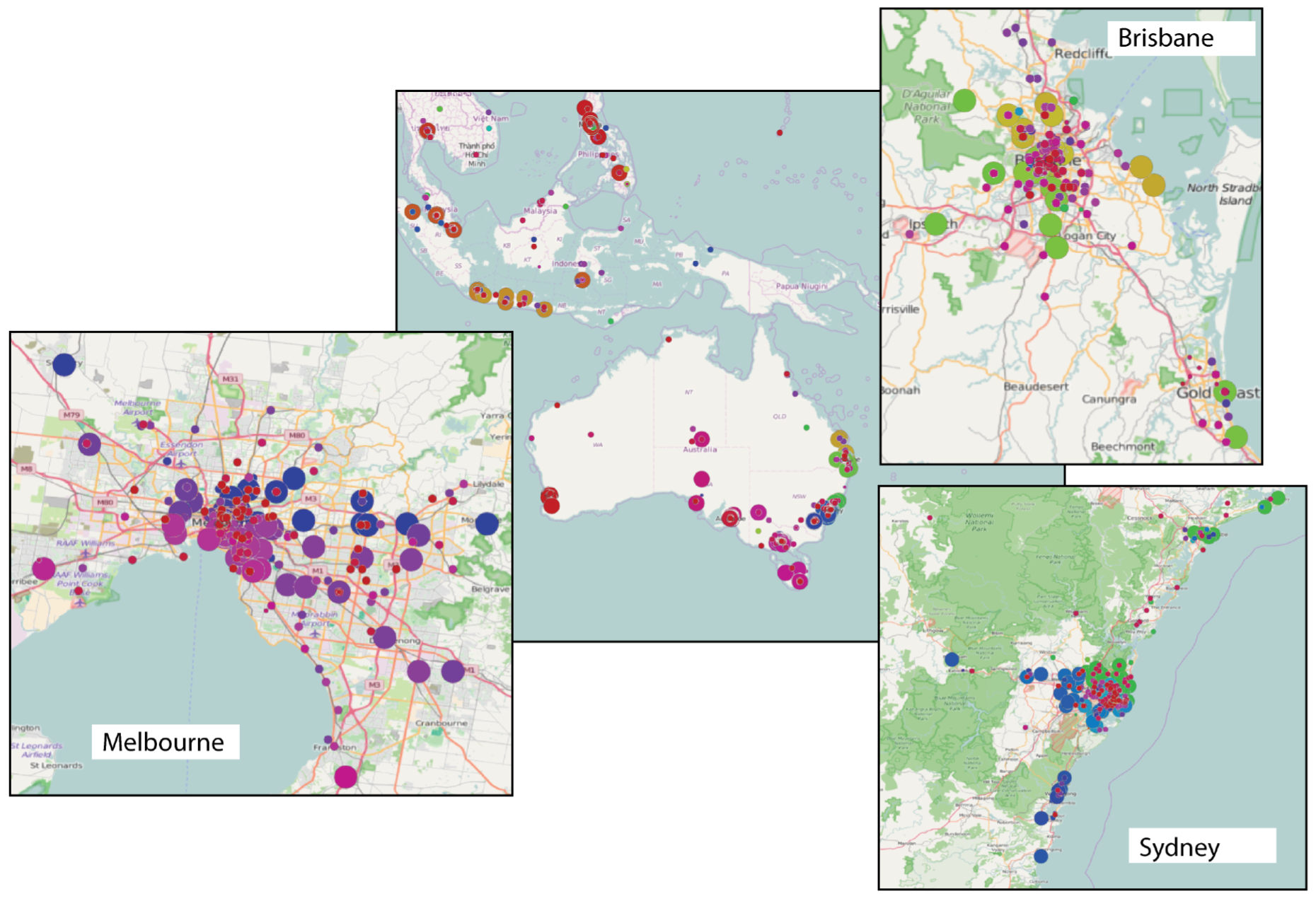
• We are overcoming the representation of a complex interconnected network as a graph by encoding the maximal cliques extracted from the same graph. The collection of maximal cliques forms a high dimensional simplicial complex that provides information about the shape, in a topological sense, of said graph. We are defining a dimension independent edge contraction operator and a new way to verify the link condition to reduce the size of a simplicial complex while preserving its homology.
• The dimension independent edge contraction has been adopted in an exploratory work for retrieving cycles and holes in the geolocalized social network. By simplifying the simplicial complex (obtained by computing the maximal cliques on the network), we can recover the missing relationships among actors participating in the network.